Removable Discontinuity Vs Asymptote : Continuity And Discontinuity Ck 12 Foundation : A hole in a graph.
Removable Discontinuity Vs Asymptote : Continuity And Discontinuity Ck 12 Foundation : A hole in a graph.. This last discontinuity is fairly common. Which we call as, removable discontinuity. In this lesson we learn how to find removable discontinuities and distinguish them from vertical asymptotes. The first condition that can occur is Because removable discontituity means that the limit of the function at that point has a finite value, and then you define the value of the function as that valu (the limit value).
Vertical asymptote or removable discontinuity. Comment #bprpyay down below & your comment might be featured in my future videos!!! The difference between a removable discontinuity and a vertical asymptote is that we have a r. Horizontal asymptote, @0:10 vertical asymptote @4:16 removable discontinuity @6:47. That is where the hole is.

However, not all functions are continuous.
If a ta point a where f(x) does not exist but lim f(x) x===> a is a number b ( not infinity) by giving f(a) t. Although at one time some sources included the requirement that the curve. You cannot meet both conditions. Calculus limits classifying topics of discontinuity (removable vs. In this video, i show an example on how to find the horizontal asymptote, vertical asymptote and removable discontinuity from a rational function. Something like removable_discontinuity = true/false. With an asymptote the limits equal infinity. Discontinuities for which the limit of f(x) exists and is finite are called removable discontinuities for reasons explained below. That is where the hole is. A removable discontinuity causes a hole in the graph. Determine the location of any removable discontinuities, vertical asymptotes, and horizontal asymptotes for the function given below. Vertical asymptote or removable discontinuity. And so we are going to be discontinuous.
The value b the discontnuity is removed. Both f(x) and g(x) have an asymptote at x = 1. In this video, i show an example on how to find the horizontal asymptote, vertical asymptote and removable discontinuity from a rational function. Transcribed image text from this question. Removable discontinuities by jocelyn providence on vimeo, the home for high quality videos and the people who love them.
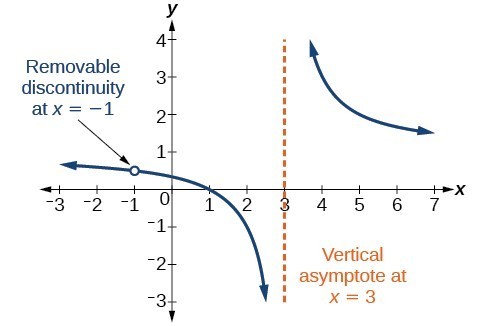
If a ta point a where f(x) does not exist but lim f(x) x===> a is a number b ( not infinity) by giving f(a) t.
Determine the location of any removable discontinuities, vertical asymptotes, and horizontal asymptotes for the function given below. Something like removable_discontinuity = true/false. Comment #bprpyay down below & your comment might be featured in my future videos!!! The value b the discontnuity is removed. This is vertical asymptotes vs. How do you find asymptotic discontinuity? Vertical asymptote or removable discontinuity. Does the function have a vertical asymptote or removable discontinuity? A removable discontinuity causes a hole in the graph. Zeros of denominator not numerator. However, not all functions are continuous. Whenever an asymptote exists, asymptotic discontinuities occur. Because removable discontituity means that the limit of the function at that point has a finite value, and then you define the value of the function as that valu (the limit value).
Transcribed image text from this question. A function f has a removable discontinuity at x = a if the limit of f(x) as x → a exists, but either f(a) does not exist, or the value of f(a) is not equal to the limiting value. Continuous functions are of utmost importance in mathematics, functions and applications. Determine the location of any removable discontinuities, vertical asymptotes, and horizontal asymptotes for the function given below. A hole in a graph.
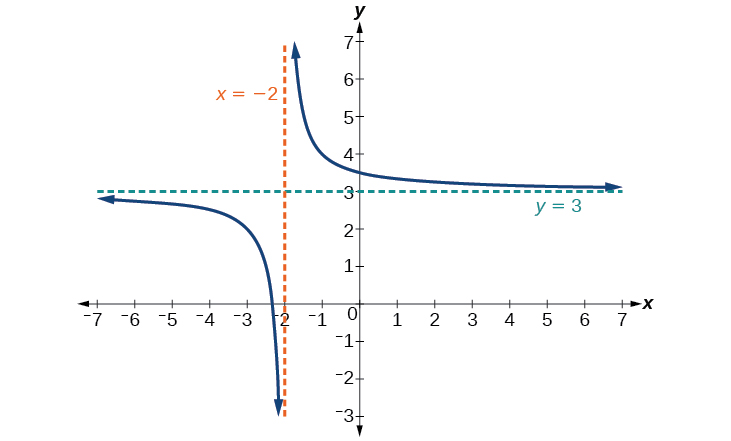
A removable discontinuity occurs when you have a rational expression with a common factors in the numerator and denominator.
In this video, i show an example on how to find the horizontal asymptote, vertical asymptote and removable discontinuity from a rational function. Whenever an asymptote exists, asymptotic discontinuities occur. At every pi/2 +kpi for cosx, the value is 0. That is, a discontinuity that can be repaired by filling in a single point. The asymptote of a curve in analytical geometry is a line whereby the distance between the line and the curve nears zero as both of them tend to infinity. A function f has a removable discontinuity at x = a if the limit of f(x) as x → a exists, but either f(a) does not exist, or the value of f(a) is not equal to the limiting value. In this lesson we learn how to find removable discontinuities and distinguish them from vertical asymptotes. Although at one time some sources included the requirement that the curve. So maybe instead removable_discontinuity=true a better name would be check_limit=true for a potential flag to add to solve(). .a removable discontinuity (a hole in the graph of the function) or a nonremovable discontinuity (such as a jump or an asymptote in the graph) : Formally, a removable discontinuity is one at which the limit of the function exists but does not equal the value of the function at that point; A removable discontinuity occurs when you have a rational expression with a common factors in the numerator and denominator. 05.10.2014 · classifying topics of discontinuity (removable vs.
Komentar
Posting Komentar